Grundkurs Mathematik
-ERSTTERMIN-
Teil A
Lösungen Aufgabe 1

Lösung: Prozess des Ziehens der Lose:
1. Losanordnung: Wir haben drei Lose: eines für den Fußballbesuch (wir nennen es „Gewinnlos“) und zwei für den Nicht-Besuch (wir nennen sie „Verlustlose“). Wir bezeichnen die Söhne als A, B und C.
2. Ziehprozess: Die Söhne ziehen nacheinander ein Los, wobei die Reihenfolge der Ziehungen nicht wichtig ist. Wir können die Ziehungen als Permutationen der drei Lose betrachten.
3. Mögliche Ergebnisse: Da jeder Sohn ein Los zieht, gibt es insgesamt 3 mögliche Reihenfolgen für das Ziehen der Lose, also 6 verschiedene Kombinationen:
- A zieht Gewinnlos, B zieht Verlustlos, C zieht Verlustlos: (G, V, V)
- A zieht Verlustlos, B zieht Gewinnlos, C zieht Verlustlos: (V, G, V)
- A zieht Verlustlos, B zieht Verlustlos, C zieht Gewinnlos: (V, V, G)
- B zieht Gewinnlos, A zieht Verlustlos, C zieht Verlustlos: (G, V, V)
- B zieht Verlustlos, A zieht Gewinnlos, C zieht Verlustlos: (V, G, V)
- B zieht Verlustlos, A zieht Verlustlos, C zieht Gewinnlos: (V, V, G)
- C zieht Gewinnlos, A zieht Verlustlos, B zieht Verlustlos: (G, V, V)
- C zieht Verlustlos, A zieht Gewinnlos, B zieht Verlustlos: (V, G, V)
- C zieht Verlustlos, A zieht Verlustlos, B zieht Gewinnlos: (V, V, G)
Die obigen Kombinationen sind nur Beispiele für die ersten beiden Positionen und zeigen, dass jeder Sohn in jeder Ziehung eine Chance hat, das Gewinnlos zu ziehen.
4. Wahrscheinlichkeiten: Jedes Los hat die gleiche Wahrscheinlichkeit, gezogen zu werden, da die Ziehungen zufällig sind. Da die Lose nicht unterscheidbar sind, sind alle Ziehungsreihenfolgen gleich wahrscheinlich.
5. Berechnung der Wahrscheinlichkeiten:
- Die Wahrscheinlichkeit, dass Sohn A das Gewinnlos zieht, ist die Anzahl der Reihenfolgen, in denen A das Gewinnlos zieht, geteilt durch die Gesamtanzahl der möglichen Ziehungen:
- A hat 2 mögliche Gewinnkombinationen: (G, V, V), (V, G, V), und (V, V, G).
- Es gibt 6 mögliche Kombinationen insgesamt.
- Daher ist die Wahrscheinlichkeit, dass A das Gewinnlos zieht: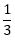
- Für Sohn B und Sohn C ist es genauso, also haben auch sie eine Wahrscheinlichkeit von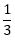 , das Gewinnlos zu ziehen.
, das Gewinnlos zu ziehen.
6. Fazit: Da jeder Sohn in jeder der 6 möglichen Kombinationen die gleiche Anzahl an günstigen Ergebnissen hat, das Gewinnlos zu ziehen, ist die Wahrscheinlichkeit für jeden Sohn gleich. Daher beträgt die Wahrscheinlichkeit für jeden Sohn, das Los für den Fußballbesuch zu ziehen,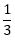 .
.
1. Losanordnung: Wir haben drei Lose: eines für den Fußballbesuch (wir nennen es „Gewinnlos“) und zwei für den Nicht-Besuch (wir nennen sie „Verlustlose“). Wir bezeichnen die Söhne als A, B und C.
2. Ziehprozess: Die Söhne ziehen nacheinander ein Los, wobei die Reihenfolge der Ziehungen nicht wichtig ist. Wir können die Ziehungen als Permutationen der drei Lose betrachten.
3. Mögliche Ergebnisse: Da jeder Sohn ein Los zieht, gibt es insgesamt 3 mögliche Reihenfolgen für das Ziehen der Lose, also 6 verschiedene Kombinationen:
- A zieht Gewinnlos, B zieht Verlustlos, C zieht Verlustlos: (G, V, V)
- A zieht Verlustlos, B zieht Gewinnlos, C zieht Verlustlos: (V, G, V)
- A zieht Verlustlos, B zieht Verlustlos, C zieht Gewinnlos: (V, V, G)
- B zieht Gewinnlos, A zieht Verlustlos, C zieht Verlustlos: (G, V, V)
- B zieht Verlustlos, A zieht Gewinnlos, C zieht Verlustlos: (V, G, V)
- B zieht Verlustlos, A zieht Verlustlos, C zieht Gewinnlos: (V, V, G)
- C zieht Gewinnlos, A zieht Verlustlos, B zieht Verlustlos: (G, V, V)
- C zieht Verlustlos, A zieht Gewinnlos, B zieht Verlustlos: (V, G, V)
- C zieht Verlustlos, A zieht Verlustlos, B zieht Gewinnlos: (V, V, G)
Die obigen Kombinationen sind nur Beispiele für die ersten beiden Positionen und zeigen, dass jeder Sohn in jeder Ziehung eine Chance hat, das Gewinnlos zu ziehen.
4. Wahrscheinlichkeiten: Jedes Los hat die gleiche Wahrscheinlichkeit, gezogen zu werden, da die Ziehungen zufällig sind. Da die Lose nicht unterscheidbar sind, sind alle Ziehungsreihenfolgen gleich wahrscheinlich.
5. Berechnung der Wahrscheinlichkeiten:
- Die Wahrscheinlichkeit, dass Sohn A das Gewinnlos zieht, ist die Anzahl der Reihenfolgen, in denen A das Gewinnlos zieht, geteilt durch die Gesamtanzahl der möglichen Ziehungen:
- A hat 2 mögliche Gewinnkombinationen: (G, V, V), (V, G, V), und (V, V, G).
- Es gibt 6 mögliche Kombinationen insgesamt.
- Daher ist die Wahrscheinlichkeit, dass A das Gewinnlos zieht:
- Für Sohn B und Sohn C ist es genauso, also haben auch sie eine Wahrscheinlichkeit von
6. Fazit: Da jeder Sohn in jeder der 6 möglichen Kombinationen die gleiche Anzahl an günstigen Ergebnissen hat, das Gewinnlos zu ziehen, ist die Wahrscheinlichkeit für jeden Sohn gleich. Daher beträgt die Wahrscheinlichkeit für jeden Sohn, das Los für den Fußballbesuch zu ziehen,